Как рассчитать эффективную процентную ставку по кредиту
Эффективная процентная ставка
Определение
Концепция эффективной процентной ставки (англ. Effective Interest Rate) используется для того, чтобы провести оценку всех затрат связанных с привлечением заемного финансирования или доходов от вложений в финансовый актив. Кроме того, требования МСФО (международных стандартов финансовой отчетности) предполагают использование эффективной процентной ставки при оценке финансовых инструментов, учитываемых по амортизированной стоимости, признании расходов и доходов по финансовым инструментам, расчете обесценения финансового актива на основе приведенной стоимости будущих денежных потоков.
Причина использования этой концепции при принятии решений заключается в том, что эффективная годовая процентная ставка может отличаться от номинальной годовой процентной ставки, указанной в договоре. Причиной несовпадения этих величин служат следующие факторы:
- количество периодов, за которое в течение года начисляются проценты;
- фактическая сумма уплаченных процентов;
- фактически понесенные расходы на выплату долга.
Формула
При проведении финансовых расчетов эффективная процентная ставка приводится к годовому формату и также может упоминаться как эффективная годовая процентная ставка или годовая эквивалентная ставка (англ. Annual Equivalent Rate).
Для оценки доходности краткосрочного финансового актива (срок обращения менее 12 месяцев) используется следующая формула:

где i – номинальная годовая процентная ставка, n – количество периодов, за которое в течение года начисляются проценты (например, если проценты начисляются ежемесячно, то n=12).
При оценке стоимости использования краткосрочного финансирования формулу эффективной годовой процентной ставки в общем виде можно записать следующим образом:
| Проценты к уплате |
| Сумма кредита |
В случае дисконтного процента формула должна быть трансформирована следующим образом:
| Проценты к уплате |
| Сумма кредита – Проценты к уплате |
При расчете эффективной процентной ставки также должны быть учтены следующие два фактора:
- Дополнительные расходы, которые по сути являются срытыми процентами.
- Условия, затрагивающие основную сумму долга. Например, наличие компенсационного остатка по кредиту уменьшает реальную располагаемую сумму.
В этом случае формулы выше должны быть скорректированы следующим образом:
| Проценты к уплате + Дополнительные расходы |
| Сумма кредита – Компенсационный остаток |
Для дисконтного процента следует воспользоваться этой формулой:
| Проценты к уплате + Дополнительные расходы |
| Сумма кредита – Проценты к уплате – Компенсационный остаток |
Примеры расчета
Пример 1
Предположим, что инвестор рассматривает возможность приобретения векселя за $9 655 со сроком погашения наступающим через четыре месяца и номиналом $10 000. В этом случае расчет эффективной годовой процентной ставки будет выглядеть следующим образом.
Проценты к получению = $10 000 – $9 655 = $345
| Ставка процента за 4 месяца = | $345 | = 3,573% |
| $9 655 |
Эффективная годовая процентная ставка = (1 + 0,03573) 12/4 – 1 = 11,107%
В этом случае мы привели наши расчеты к годовой эквивалентной ставке с учетом концепции сложных процентов.
Пример 2
Компания GFL LTD рассматривает различные варианты финансирования потребности в оборотном капитале в размере $100 000. Существует возможность взять банковский кредит на следующих условиях:
- период кредитования 1 год;
- номинальная годовая процентная ставка 12%;
- единовременная комиссия за рассмотрение кредитной заявки и открытие кредитного счета 2% от суммы кредита;
- компенсационный остаток $15 000.
Проценты к уплате = $100 000 × 12% = $12 000
Дополнительные расходы = $100 000 × 2% = $2 000
| Эффективная годовая процентная ставка = | $12 000 + $2 000 | = 16,471% |
| $100 000 – $15 000 |
Пример 3
Корпорация Tristan Inc. имеет банковский кредит, который был взят на следующих условиях:
- сумма кредита $250 000;
- период кредитования 1 год;
- дисконтный процент при номинальной годовой процентной ставке 15%;
- расходы открытие кредитного счета 1% от суммы кредита;
- компенсационный остаток $50 000.
| Проценты к уплате = $250 000 – | $250 000 | = $32 608,70 |
| (1+0,15) 1 |
Дополнительные расходы = $250 000 × 1% = $2 500
8. Расчет эффективной процентной ставки
В некоторых случаях при выдаче ссуды на долгосрочный период кредиторы могут поставить условие, чтобы проценты по ссуде выплачивались не ежегодно, а чаще, например каждые полгода, каждую четверть года или каждый месяц. Процентные ставки, по которым производятся более частые начисления процентов, обычно определяются на основе годовых процентных ставок. Если каждые полгода начисляется 10 %, годовая процентная ставка будет 20 % в год.
Годовую процентную ставку называют номинальной (обозначается i). Эффект от более частого начисления процентов заключается в том, что подлинная эффективная процентная ставка в итоге за год выше, чем номинальная процентная ставка.
Формула для расчета эффективной процентной ставки при помощи номинальной процентной ставки выглядит следующим образом:
iэ = (1 + i / с) c – 1, (12)
где iэ – эффективная процентная ставка;
с – количество раз начисления процентов в течение одного процентного периода.
Например, определить эффективную годовую процентную ставку при условии, что номинальная ставка равна 10 % в год и начисление процентов ведется раз в месяц:
iэ = [(1 + 0,10 / 12) 12 – 1] х· 100 % = 10,47 %.
Проценты могут начисляться 2, 4, 12 раз в год. Как предел они могут начисляться бесконечное число раз в год, т. е. непрерывно. В этих условиях процентная ставка короткого отрезка времени стремится к нулю.
Когда проценты начисляются непрерывно эффективная годовая процентная ставка рассчитывается по формуле:
где е – основание натурального логарифма, е = 2,7182.
Поскольку эффективная годовая процентная ставка представляет подлинные проценты, эта ставка должна использоваться для сравнения преимуществ разных процентных ставок при использовании кредита в инвестиционных проектах.
В табл. 8.1 приведены сравнительные эффективные годовые процентные ставки, соответствующие номинальной годовой процентной ставке 70 %.
Таблица 8.1 Расчет величины эффективной годовой процентной ставки
Частота начисления процентов
Количество процентных периодов в год
Процентная ставка на короткий период
Эффективная годовая процентная ставка
В контрольной работе следует рассчитать величину эффективной процентной ставки для процентных ставок, указанных в графе 3 и 4 табл. П.3.
Частота начисления процентов для всех вариантов принимается:
По окончании расчетов сделать соответствующие выводы.
9. Сравнение вариантов кредитования
В этой задаче необходимо сопоставить два варианта кредитования:
I вариант – обеспечивает равномерный возврат кредита в течение 12 месяцев.
II вариант – равномерный возврат кредита с начислением процентов на оставшуюся сумму.
Оба варианта рассчитываются на величину, указанную в графе 2 табл. П.3, ставка процента принимается на уровне 2–4 % в месяц (графа 5 табл. П.3), продолжительность кредитования – 12 месяцев.
Исходные данные для примера расчета вариантов кредитования
Величина кредита 170,33 тыс. руб.;
ставка процента в месяц 3,00 %;
продолжительность кредитования 12 месяцев.
В графе 1 таблиц 9.1 и 9.2 указываются номера месяцев по порядку. В графе 2 таблиц 9.1 и 9.2 «Остаток на начало месяца» указывается сумма кредита, которую необходимо вернуть. Она рассчитывается как разность значений, указанных в графе 4 и графе 6 (или графой 2 (значение за прошлый месяц) и графой 5 таблиц 9.1 и 9.2).
Величина процентов, выплачиваемых ежемесячно, указывается в графе 3 таблиц 9.1 и 9.2 и определяется от величины остатка кредита на начало месяца (графа 2). Остаток общей задолженности представляет собой величину кредита вместе с процентами и определяется суммой граф 2 и 3 таблиц 9.1 и 9.2.
В первом варианте расчет величины платы за кредит вместе с процентами, (графа 6 табл. 10) производится по формуле аннуитета (А):
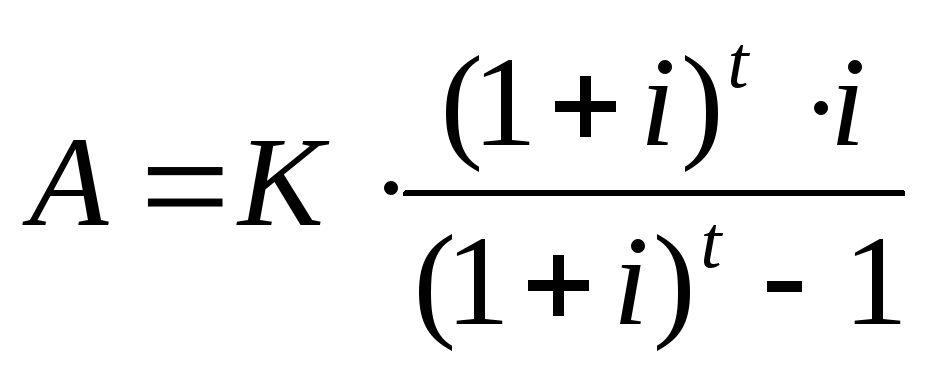 , (14)
, (14)
где К – величина кредита, млн. руб.;
t – количество месяцев кредитования;
i – процентная ставка в месяц.
Аннуите́т — общий термин, описывающий график погашения кредита(выплаты вознаграждения или уплаты части основного долга и процентов по нему), когда выплаты устанавливаются периодически равными суммами через равные промежутки времени.
Сумма аннуитетного платежа включает в себя основной долг и вознаграждение.
В широком смысле, аннуитетом называется как сам кредит, так и сумма периодического платежа, вид графика погашения кредита.
Суммы возврата кредита (графа 5 табл. 9.1) определяются как разность между величиной ежемесячной выплаты (возврат кредита + проценты, графа 6 табл. 9.1) и величиной процентов, которые необходимо выплатить в этом месяце.
Таблица 9.1 Равномерный возврат кредита в течение 12 месяцев
Самостоятельный расчет Эффективной Процентной Ставки

Чтож, давайте попробуем рассчитать эффективную процентную ставку своими силами. Для того чтобы осилить это дело потребуется не только вооружиться калькулятором и программой Excel, но и немного наморщить мозг, ибо для рассчета сумм и порядка кредитных платежей нам потребуется освоить некоторые финансовые формулы, которые “для простых смертных” могут показаться не такими уж и очевидными.
Как самостоятельно посчитать эффективную процентную ставку?
Давайте возьмем конкретный пример и рассчитаем его.
Исходные данные:
- Сумма кредита: $100 000
- Годовая ставка: 18%
- Комиссия за обслуживание кредита: 1% от суммы (взимается ежемесячно)
- Срок кредитования: 12 месяцев
- Метод погашения: аннуитетные платежи.
Аннуитетный платеж означает, что, погашать кредит нужно равными долями в течение всего срока кредитования. Или, попросту говоря, ежемесячно необходимо выплачивать одинаковую сумму. На мой взгляд это наиболее удобный способ погашения кредита.
Для начала – узнаем размер ежемесячного платежа. Для этого нам потребуется формула, приведенная в статье “Аннуитетные платежи”.
Напомним, формула выглядит так:
A = K*S, где S – сумма кредита (в нашем случае S = 100 000); K – коэффициент аннуитета, рассчитывается по формуле, зависит от величин i и n.
В данном случае i = 0,015 n = 12. Если мы подставим полученные значения в вышеприведенную формулу, то получим, что
К = 0,09168.
А = $9168.
Однако, можно сделать немного проще. Для того, чтобы рассчитать размер ежемесячного платежа, воспользуемся встроенной в Excel функцией ПЛТ.
Вводим в ячейку формулу вида:
И получаем ту же сумму: $9168.
Теперь нам нужно составить в Excel’е таблицу ежемесячных платежей:
| Cкачать таблицу расчёта в формате Excel |
Если вы не до конца поняли, как происходит рассчет – перечитайте статью и смотрите на формулы в строке состояния Excel
Так же обратите внимание, что с каждым месяцем выплаты процентов по кредиту уменьшаются, а выплаты основной части кредита увеличиваются. Это одна из особенностей аннуитетного способа погашения кредита.
Итоги расчета эффективной процентной ставки
- Мы взяли кредит на $100 000.
- Выплатили $122015,99.
- Переплата составила $22015,99.
- Ставка 22015,99 / 100000 = 22%.
Ежемесячная комиссия в 1% обошлась нам в 12000 долларов, что превышает основную сумму выплат по кредиту! Почему так? Потому что комиссию за обслуживание мы каждый месяц платили из рассчета от основной суммы кредита ($100’000), а проценты с каждым месяцем уменьшались ввиду того, что ежемесячно уменьшалась сумма кредита. Как видите, такая, безобидная, на первый взгляд, хитрость банка, как процент за обслуживание при ближайшем рассмотрении обходится очень дорого.
Хомячковый рай. Уйти и потеряться:
Формула эффективной процентной ставки
Секрет эффективной процентной ставки сокрыт в указаниях Центробанка РФ № 2008-У «О порядке расчета и доведения до заемщика (физического лица) полной стоимости кредита», датированных 13 мая 2008 года. Оптимальная процентная ставка в виде формулы представлена таким образом:
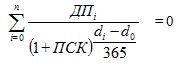
- di – дата первого финансового потока;
- d0 – дата выдачи суммы кредита;
- n – количество финансовых потоков;
- ДПi – сумма первого финансового потока, прописанная в договоре;
- ПСК – полная стоимость кредита с учетом годовых процентов.
Не менее популярным инструментом для расчета выгодной процентной ставки по версии Центробанка остается программа Excel, в частности ее формула ЧИСТВНДОХ.
Как вы имели возможность убедиться самостоятельно, даже блестящие знания школьного курса математики вряд ли помогут «непосвященным» заемщикам разобраться в сложностях подсчета эффективной процентной ставки. Стоит отметить, что даже если вы осмелитесь наперевес с калькулятором штурмовать финансовые вершины банковских подсчетов, то все равно вряд ли добьетесь нормальных результатов. Все причина в том, что непростая система «скрытых» комиссий наравне со спецификой оборота средств в финансовых учреждениях слишком сложна и непрозрачна, чтобы типичный пользователь мог разобраться в ней самостоятельно.
Так что «розовая» мечта самостоятельно просчитать кредитные ставки и обезопасить себя от чрезмерных выплат для многих плательщиков навсегда останется таковой. Эффективную банковскую ставку, рассчитанную по методике ЦБ, разумно использовать разве что для сравнения аналогичных предложений от разных банков для выбора оптимального вида платежей.
Хомячковый рай. Уйти и потеряться:
Эффективная процентная ставка (ЭПС). Расчёт ставки по кредиту

Обычно банки в борьбе за клиентов предлагают невероятно выгодные условия, особенно в отношении кредитов. Многие рекламные материалы строятся на том, что процентные ставки по кредитам именно в этом банке наиболее низкие. Конкретную величину этой ставки, действительно очень привлекательную, часто изображают в качестве одного из основных элементов рекламной композиции буклета или постера. Но почти никто не удосуживается прочитать сносочку где-нибудь внизу или сбоку, которая поясняет, что процентная ставка, – это еще не все и в дополнение к ней существуют всевозможные комиссионные платежи, количество и наименования которых зависят лишь от фантазии банкира. Поэтому будущему клиенту банка очень полезно разобраться, какова же реальная стоимость кредита, то есть рассчитать эффективную процентную ставку (сокращенно – ЭПС).
Очевидно, что из-за нежелания потерять даже малую часть прибыли банки идут на различные уловки и ухищрения. Поэтому объявленная и реальная кредитные процентные ставки могут отличаться отнюдь не на доли процентов и конечно не в пользу клиента.
Величина эффективной процентной ставки позволяет сравнить реальные кредитные условия различных банковских учреждений и провести их объективную оценку.
Как рассчитать эффективную процентную ставку кредитной карты
Если взять в качестве простого примера известную всем кредитную карту, то, рассчитывая ЭПС по ней, следует учитывать комиссии банка – за ведение счета, за обслуживание самой карты и пр. Если банком предлагается льготный кредитный период, то рассчитывать ЭПС необходимо для обоих вариантов – с льготой и без нее. Поскольку поведение заемщика предугадать очень сложно, при расчете ЭПС кредитной карты принимаются такие начальные условия: лимит кредитования и размер задолженности равны, платежи вносятся равными долями, срок кредита – 24 месяца.
В итоге получается, что точную величину ЭПС кредитной карты высчитать можно только приблизительно, в основном из-за непредсказуемости действий заемщика. Но в любом случае эта цифра будет намного больше заявленной банком.
Расчет ЭПС
В общем виде расчет эффективной процентной ставки ведется согласно методики, утвержденной в Положении 254-П Центробанка России. При этом обязательно следует учитывать все сборы, проценты и комиссии, уплачиваемые заемщиком банку.
Как рассчитать эффективную процентную ставку по кредиту


Горячая линия
Коллекторы, банкротство, открытие ООО или ИП и др.
Мы поможем!
Курсы валют
| Курс ЦБ | |||||
|
|
| Биржевой курс | |||||
|
|
Определение и сущность
 Суть ставки, называемой эффективной, достаточно проста и понятно. Она выражает действительную стоимость получаемого займа с позиции, занимаемой заемщиком.
Суть ставки, называемой эффективной, достаточно проста и понятно. Она выражает действительную стоимость получаемого займа с позиции, занимаемой заемщиком.
А именно, при ее расчете берутся во внимание не только платежи по кредиту, а все дополнительные выплаты, связанные с ссудой.
В данном случае, к побочным оплатам можно отнести наличие «скрытых» банковских комиссий, начисляемых за то, чтоб открыть и далее вести счет, провести наличные средства через кассу и другие. При получении ипотеки на жилье или автокредите клиент обязан оформить страховку на приобретаемый объект, которая также станет дополнительной выплатой, хотя ее получит не банк, а страховщик.
Центробанк в законном порядке обязал коммерческие банковские структуры не скрывать размер эффективной ставки по процентам, для чего была разработана специальная формула. Однако, не последовало четких указаний относительно наименования платежей, входящих в этот расчет. Поэтому каждый банк имеет свою точку зрения по этому вопросу.
К примеру, оплата страховых взносов у многих кредиторов не входит в расчеты. Все же, более верным и более справедливым будет тот подход, гдеучитываются все обязательные платежи для выбранного вида кредитования, включая страховые взносы.
Не секрет, что, сталкиваясь с оформлением займа, клиент должен вникать в некоторые понятия, встречающиеся на рынке кредитования.
Номинальная и эффективная процентные ставки — в чем отличие?
Первая не меняется на протяжении всего срока кредитования и именно она оглашается клиенту как одно из основных условий конкретно выбранной кредитной программы.
 Предположим, при ссуде в 1000 рублей за год заемщиком выплачивается 250 рублей. В данном варианте размер номинальной ставки 25% за 12 месяцев. А вот какую прибыль в данном случае получает банк – это второй вопрос, все зависит от размера инфляции, может 20%, а может всего 5%. Заемщика это мало интересует.
Предположим, при ссуде в 1000 рублей за год заемщиком выплачивается 250 рублей. В данном варианте размер номинальной ставки 25% за 12 месяцев. А вот какую прибыль в данном случае получает банк – это второй вопрос, все зависит от размера инфляции, может 20%, а может всего 5%. Заемщика это мало интересует.
Гораздо полезней, получая заем знать, сколько же на самом деле он стоит и здесь без применения эффективной ставки не обойтись. Она даст представление о том, каков совокупный размер всех надбавок будет добавлен к телу кредита и сколько на самом деле придется оплачивать.
По сути, данная ставка реально характеризует кредит и по ней можно сравнить все предполагаемые варианты займов.
Расчет эффективной годовой процентной ставки по формуле
Для вычисления годовой процентной ставки прежде всего необходимо выяснить какова сумма ежемесячного платежа.
Воспользуемся формулой, при условии, что выплаты проводятся равными частями:
- А – ежемесячный платеж;
- S — сумма займа;
- K — коэффициент аннуитетного кредита, рассчитываетсяс помощью формулы, зависящей от iмесячной ставки по кредиту и n,параметра, определяющего число периодов, по завершении которых будет выплачен кредит:
K = i*(1+i)*n/ (1+i)*n-1
Зная коэффициент К, несложно вычислить значение А (ежемесячную оплату) и далее умножив ее на количество месяцев в кредите узнать реальную стоимость займа.
Значение эффективной процентной ставки можно выяснить, если разделить сумму переплаты по займу на сумму предполагаемого или уже взятого кредита.
Примерный расчет по кредиту
Для лучшего понимания рассмотрим пример расчета эффективной годовой процентной ставки.
Предположим, что взят кредит на 200000 рублей со ставкой 18%, сроком на год и ежемесячной комиссией за кассовое обслуживание 1%.
Метод выплат кредита аннуитетный. Значит:
S–200000 рублей;
n – 12 месяцев;
i – 1,5% за месяц (18% ставка деленная на срок кредита12 месяцев).
Определяем K – коэффициент аннуитетного кредита по выше приведенной формуле:
K=0,015*(1+0,015)*12(1+0,015)*12-1=0,09168
Значит ежемесячный платеж, следуя формуле A = K*S равен,
A=200000*0,09168=18336 рубля оплата за месяц
С учетом 1% кассового обслуживания, насчитываемого на сумму займа, получается, что ежемесячная плата составит:
Стоимость займа за год: 20336*12 месяцев = 244032 рубля,
Размер переплаты по кредиту 44032 рубля.
Из этого следует, что по факту ставка кредита за год:
44032/200000= 0,22 или 22%.
Трудно применить какую-то одну формулу для подобного расчета. Для простоты можно использовать калькулятор на сайте выбранного банка.
Но нужно знать, что каждое кредитное учреждение применяет свои условия и вводит комиссии на займы согласно своей выгоде и кстати, это законно.
Кроме того, по закону кредитор обязан информировать клиентов обо всех возможных дополнительных платежах. Поэтому на пункте, освещающем эффективную ставку по займу всегда следует делать особый акцент.
 Загрузка.
Загрузка.














