Как найти процент от числа правило

Нахождение процента от числа

Разделы: Математика

Цели: познакомить учащихся с задачами на нахождение процента от числа, научить находить процент от числа двумя способами, развивать умение работать самостоятельно, воспитывать потребность и умение учиться математике.

1. Организационный момент.

2. Устно:

Задание № 1. Закончите предложение:

1. 1% от рубля называется…
2. 1% от метра называется…
3. 1% от дециметра называется…
4. 1% от квадратного дециметра называются….

Задание № 2. Верно ли что:

1. 345 человек составляют меньше 1% от 10000 человек?
2. 345 р. составляют менее 1% от 20000 р.?
3. 8,2% равны 0,82?
4. 1,3 равны 130%?

Задание № 3. Сравните результаты:

1. 150 р. увеличили на 50% и 100 р. увеличили на 100%; 100 р. увеличили на 25% и 150 р. уменьшили на 20%

* Задание № 4. Незнайку попросили число 20 сначала уменьшить на 10%, а потом увеличить на 10%. “Тут нечего и решать! – сказал Незнайка – Ясно, что получится число 20.” Прав ли Незнайка?

3. Сообщение темы урока.

Мы уже умеем с вами находить некоторые проценты от числа. Какие?

– 10%. Это десятая часть числа. Нужно число разделить на 10.

– 20%. Это пятая часть числа. Нужно число разделить на пять.

– 25%. Это четвертая часть числа. Нужно число разделить на четыре.

– 50%. Это половина числа. Нужно число разделить на два.

Но очень часто в повседневной жизни приходится находить 6,4%, 16%, 42% числа. Сегодня на уроке мы с вами научимся, как это сделать.

4. Изучение нового материала.

Подумайте, как нам решить такую задачу?

Задача № 1. Вкладчик положил в банк 10000 р. под 7 % годовых. На сколько увеличится его вклад через 1 год? А если процент банка составляет 9%, 10,5% в год?

С помощью учащихся рассмотреть два способа решения задачи.

1 способ. 1) 10000: 100 = 100(р.) составляет 1%;

2) 100 · 7 = 700 (р.) составляют 7%;

3) 100 · 9 = 900 (р.) составляют 9%;

4) 100 · 10,5 = 1050 (р.) составляют 10,5%.

2 способ. 1) 7% = 0,07;

2) 10000 · 0,07 = 700 (р.) составляют 7%;

3) 10000 · 0,09 = 900 (р.) составляют 9%;

4) 10000 · 0,105 = 1050 (р.) составляют 10,5%.

Ответ: на 700 р., 900 р., 1050 р.

Вывод: Как найти процент от числа?

– найти 1% числа и умножить его на число процентов;

– представить процент в виде десятичной дроби и умножить ее на данное число.

5. Отработка полученных правил.

Устно: Как найти:

Задача № 2. (самостоятельно)

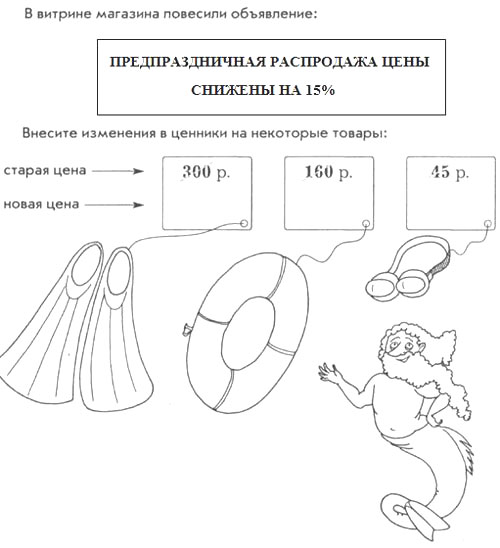
Стоимость ласт:

1. 300 • 0,15 = 45 (р.) – 15%
2. 300 – 45 = 255 (р.) – новая стоимость.

Стоимость круга:

1. 160 • 0,15 = 24 (р.) – 15%
2. 160 – 24 = 136 (р.) – новая стоимость.

Стоимость очков:

1. 45 • 0,15 = 6,75 (р.) – 15%
2. 45 – 6,75 = 38,25 (р.) – новая цена.

– Как можно было решить эту задачу другим способом?

Например, стоимость ласт:

1) 100% – 15% = 85% составляет новая цена от старой;

2) 300 · 0,85 = 255 (р.) стоят ласты.

Задача № 3. (Самостоятельно)

Папа положил в банк 15000 рублей под 9,5% годовых, а мама 16000 рублей под 8,5% годовых. У кого из них через год на вкладе денег будет больше?

Решение:

1. 15000 · 0,095 = 1425 (р.) составляют 9,5%;
2. 15000 + 1425 = 16425 (р.) через год у папы;
3. 16000 · 0,085 = 1360 (р.) составляют 8,5%;
4. 16000 + 1360 = 17360 (р.) через год у мамы;
5. 17360 > 16425.

Ответ: через год на счете денег будет больше у мамы.

6. Итог урока.

– чему мы научились сегодня на уроке?

– для чего нужно уметь находить процент от числа?

Как найти процент от числа

Процент показывает сотую часть единицы, которую обозначают с помощью знака «%». Данный показатель используется, чтобы обозначить долю чего-либо к целому. Как посчитать процент от числа еще знали в Древнем Риме. До того, как придумали десятичную систему исчисления, вычисления производились с помощью дробей, которые были кратны 1 к 100. Октавиан Август брал налог в размере одной сотой на товары, которые продавались на аукционе, и назывался Centesima Rerum Venalium. Расчеты с помощью множителей чем-то напоминали вычисление процентов.

При замене валюты в средние века вычисления со знаменателем сто стали более распространенными, а с конца 16 века до начала 17 века такой метод расчета стал использоваться всеми, исходя из материалов, которые содержат арифметические вычисления. Согласно материалам такой метод применяли при расчете прибыли и убытка, процентной ставки, а также при правиле трёх. В семнадцатом веке эта форма вычислений была стандартом для оформления процентных ставок в сотых долях. Понятие процент в Росcии ввел Пётр I. Однако считается, что похожие вычисления начали использовать в Смутное время, в результате первой привязки чеканных монет 1 к 100, когда рубль стоил 10 гривенников, а немного позднее — 100 копеек.

Иногда сравнивают две величины не сравнивая их значения, а в процентах. К примеру, цену двух товаров сравнивать не в денежном эквиваленте, а сравнить в процентах насколько цена одного товара превышает цену другого. Если можно определить, насколько один показатель больше или меньше другого, то для сравнения в % необходимо указать, относительно какой величины вычисляется процент. Такое указание иногда не нужно, в том случае, когда говорится, что один показатель больше другого на число процентов, которое больше показателя 100. В таком случае есть один способ найти процент, поделить разность на меньшее из двух чисел и умножить это число на 100.

Как находить процент от числа

Для того, чтобы находить процент от числа, нужно данное число умножить на число процентов и полученное число разделить на сто. как правило, выделяют три основных вида задач на вычисление процентов:

• Посчитать процент от данного числа. Данное число нужно умножить на указанное число процентов, а затем результат нужно поделить на 100.
• Определить число по заданному другому числу и его величине в процентах от искомого числа. Данное число нужно поделить на процентное выражение и результат умножить на 100.
• Определить выражение одного числа от другого в процентах. Первое число нужно поделить на второе и результат умножить на 100.

Как правило, в экономике, где большинство показателей выражают в процентах, изменение таких показателей выражается не в % от исходного показателя, а в процентных пунктах, которые показывают разницу нового и старого значений показателя. К примеру, если в стране индекс деловой активности повысился с 50% до 51%, то его изменения вычисляют подобным образом: (51%-50%)/50= 1/50=2%, что в процентных пунктах составляет 1%.

Я всегда, чтобы найти процент от числа умножаю, например, на 0.2 (20%), 0.5 (50%) ну и так далее. Понятно, что это сначала делится на 100, а потом умножается на нужный процент, но перестраиваешься и потом, как найти процент от числа доходит до автомата.

Кстати, на днях прочитал еще один способ, как можно найти процент от числа. Например, если нужно найти 60% от 400, для этого нужно разделить оба числа на 10, таким образом получим 6 и 40 и перемножить их, что получится 240. Для проверки 60% от 400 (где 400 — это 100%), получается 60 раз по 4 (где 4 — это 1%), получается 60 х 4 = 240.

Такая методика нахождения процента от числа тоже работает. Хороший метод для быстрого подсчета неочевидных процентных долей.

Как найти процент от числа правило

Калькулятор процентов поможет вам рассчитать процент от числа и вычислить отношение двух чисел.

Нахождение процента от числа

Процентом называют одну сотую часть.

Рассмотрим алгоритм нахождение 15% от числа 220:

• 1 Число 220 это 100%, найдем 1% от числа, для этого разделим 220 на 100:
  1% от числа равен 220 ÷ 100 = 2.2
• 2 Чтобы найти 15%, умножим значение 1% от числа на 15. 15% от числа равно 2.2 × 15 = 33.
• 3 В итоге получаем что 15% от числа 220 равно 33%.Полностью нахождения 15% от числа можно записать: 220 ÷ 100 × 15 = 2.2 × 15 = 33

Пример Вычислить 10%, 30%, 50% от числа 760.

10% от числа равно: 760 ÷ 100 × 10 = 7.6 × 10 = 76

30% от числа равно: 760 ÷ 100 × 30 = 7.6 × 30 = 228

50% от числа равно: 760 ÷ 100 × 50 = 7.6 × 50 = 380

Рассмотрим пример когда нужно вычислить общее количество предметов, если известна часть.

Пример В корзине осталось 6 яблок, 15% от общего числа, вычислите общее количество яблок.

Найдем чему равен 1% и умножим на 100:

100% от числа равно: 6 ÷ 15 × 100 = 0.4 × 100 = 40

Отношение чисел

Частное двух чисел называют отношением этих чисел.

Рассмотрим на примерах как находить отношение двух чисел.

Пример Найдем отношение чисел 4 и 20

Число 4 составляет 20% от числа 20. Для вычисления разделим 4 на 20 и умножим на 100, получим 4 ÷ 20 × 100 = 20%

Число 20 составляет 500% от числа 4. Для вычисления разделим 20 на 4 и умножим на 100, получим 20 ÷ 4 × 100 = 500%

Из числа 4 получим 20 увеличив на 400%. Для вычисления разделим 20 на 4, умножим на 100 и отнимем 100%, получим 20 ÷ 4 × 100 – 100 = 400%

Из числа 20 получим 4 уменьшив число на 80%. Для вычисления разделим 4 на 20, умножим на 100 и отнимем 100%, получим 4 ÷ 20 × 100 – 100 = -80%. Если в результате получается отрицательное значение, то число надо уменьшать, если положительно то увеличивать.

Найдем отношение двух вещественных чисел.

Пример Найдем отношение чисел 0.3 и 0.6

Число 0.3 составляет 50% от числа 0.6. Для вычисления разделим 0.3 на 0.6 и умножим на 100, получим 0.3 ÷ 0.6 × 100 = 50%

Число 0.6 составляет 200% от числа 0.3. Для вычисления разделим 0.6 на 0.3 и умножим на 100, получим 0.6 ÷ 0.3 × 100 = 200%

Из числа 0.3 получим 0.6 увеличив на 100%. Для вычисления разделим 0.6 на 0.3, умножим на 100 и отнимем 100, получим 0.6 ÷ 0.3 × 100 – 100 = 100%

Из числа 0.6 получим 0.3 уменьшив число на 50%. Для вычисления разделим 0.3 на 0.6, умножим на 100 и отнимем 100, получим 0.3 ÷ 0.6 × 100 – 100 = -50%.

Как найти процент от числа правило

Калькулятор процентов поможет вам рассчитать процент от числа и вычислить отношение двух чисел.

Нахождение процента от числа

Процентом называют одну сотую часть.

Рассмотрим алгоритм нахождение 15% от числа 220:

• 1 Число 220 это 100%, найдем 1% от числа, для этого разделим 220 на 100:
  1% от числа равен 220 ÷ 100 = 2.2
• 2 Чтобы найти 15%, умножим значение 1% от числа на 15. 15% от числа равно 2.2 × 15 = 33.
• 3 В итоге получаем что 15% от числа 220 равно 33%.Полностью нахождения 15% от числа можно записать: 220 ÷ 100 × 15 = 2.2 × 15 = 33

Пример Вычислить 10%, 30%, 50% от числа 760.

10% от числа равно: 760 ÷ 100 × 10 = 7.6 × 10 = 76

30% от числа равно: 760 ÷ 100 × 30 = 7.6 × 30 = 228

50% от числа равно: 760 ÷ 100 × 50 = 7.6 × 50 = 380

Рассмотрим пример когда нужно вычислить общее количество предметов, если известна часть.

Пример В корзине осталось 6 яблок, 15% от общего числа, вычислите общее количество яблок.

Найдем чему равен 1% и умножим на 100:

100% от числа равно: 6 ÷ 15 × 100 = 0.4 × 100 = 40

Отношение чисел

Частное двух чисел называют отношением этих чисел.

Рассмотрим на примерах как находить отношение двух чисел.

Пример Найдем отношение чисел 4 и 20

Число 4 составляет 20% от числа 20. Для вычисления разделим 4 на 20 и умножим на 100, получим 4 ÷ 20 × 100 = 20%

Число 20 составляет 500% от числа 4. Для вычисления разделим 20 на 4 и умножим на 100, получим 20 ÷ 4 × 100 = 500%

Из числа 4 получим 20 увеличив на 400%. Для вычисления разделим 20 на 4, умножим на 100 и отнимем 100%, получим 20 ÷ 4 × 100 – 100 = 400%

Из числа 20 получим 4 уменьшив число на 80%. Для вычисления разделим 4 на 20, умножим на 100 и отнимем 100%, получим 4 ÷ 20 × 100 – 100 = -80%. Если в результате получается отрицательное значение, то число надо уменьшать, если положительно то увеличивать.

Найдем отношение двух вещественных чисел.

Пример Найдем отношение чисел 0.3 и 0.6

Число 0.3 составляет 50% от числа 0.6. Для вычисления разделим 0.3 на 0.6 и умножим на 100, получим 0.3 ÷ 0.6 × 100 = 50%

Число 0.6 составляет 200% от числа 0.3. Для вычисления разделим 0.6 на 0.3 и умножим на 100, получим 0.6 ÷ 0.3 × 100 = 200%

Из числа 0.3 получим 0.6 увеличив на 100%. Для вычисления разделим 0.6 на 0.3, умножим на 100 и отнимем 100, получим 0.6 ÷ 0.3 × 100 – 100 = 100%

Из числа 0.6 получим 0.3 уменьшив число на 50%. Для вычисления разделим 0.3 на 0.6, умножим на 100 и отнимем 100, получим 0.3 ÷ 0.6 × 100 – 100 = -50%.